判别多维标度特征学习

doi:10.11772/j.issn.1001-9081.2022030419

《计算机应用》唯一官方网站 ›› 2023, Vol. 43 ›› Issue (5): 1323-1329.DOI: 10.11772/j.issn.1001-9081.2022030419

所属专题：第九届中国数据挖掘会议(CCDM 2022)

• 第九届中国数据挖掘会议 • 下一篇

判别多维标度特征学习

唐海涛¹^,², 王红军¹^,²(), 李天瑞¹^,²

^1.西南交通大学计算机与人工智能学院，成都 611756
^2.综合交通大数据应用技术国家工程实验室（西南交通大学），成都 611756

收稿日期:2022-04-01 修回日期:2022-05-16 接受日期:2022-05-19 发布日期:2023-05-08 出版日期:2023-05-10
通讯作者: 王红军
作者简介:唐海涛（1999—），男，四川南充人，硕士研究生，CCF会员，主要研究方向：特征学习、聚类
王红军（1977—），男，四川广安人，副研究员，博士，CCF高级会员，主要研究方向：机器学习、集成学习、数据挖掘 wanghongjun@swjtu.edu.cn
李天瑞（1969—），男，福建莆田人，教授，博士，CCF杰出会员，主要研究方向：粗糙集、粒计算、云计算、数据挖掘。
基金资助:
国家重点研发计划项目(2020AAA0105101);国家自然科学基金资助项目(61773324)

Discriminative multidimensional scaling for feature learning

Haitao TANG¹^,², Hongjun WANG¹^,²(), Tianrui LI¹^,²

^1.School of Computing and Artificial Intelligence，Southwest Jiaotong University，Chengdu Sichuan 611756，China
^2.National Engineering Laboratory of Integrated Transportation Big Data Application Technology （Southwest Jiaotong University），Chengdu Sichuan 611756，China

Received:2022-04-01 Revised:2022-05-16 Accepted:2022-05-19 Online:2023-05-08 Published:2023-05-10
Contact: Hongjun WANG
About author:TANG Haitao， born in 1999， M. S. candidate. His research interests include feature learning， clustering.
WANG Hongjun， born in 1977， Ph. D.， associate research fellow. His research interests include machine learning， ensemble learning， data mining.
LI Tianrui， born in 1969， Ph. D.， professor. His research interests include rough set， granular computing， cloud computing， data mining.
Supported by:
National Key Research and Development Program of China(2020AAA0105101);National Natural Science Foundation of China(61773324)

摘要/Abstract

摘要：

传统多维标度方法学习得到的低维嵌入保持了数据点的拓扑结构，但忽略了低维嵌入数据类别间的判别性。基于此，提出一种基于多维标度法的无监督判别性特征学习方法——判别多维标度模型（DMDS），该模型能在学习低维数据表示的同时发现簇结构，并通过使同簇的低维嵌入更接近，让学习到的数据表示更具有判别性。首先，设计了DMDS对应的目标公式，体现所学习特征在保留拓扑性的同时增强判别性；其次，对目标函数进行了推理和求解，并根据推理过程设计所对应的迭代优化算法；最后，在12个公开的数据集上对聚类平均准确率和平均纯度进行对比实验。实验结果表明，根据Friedman统计量综合评价DMDS在12个数据集上的性能优于原始数据表示和传统多维标度模型的数据表示，它的低维嵌入更具有判别性。

关键词: 判别性特征学习, 多维标度法, 降维, 模糊聚类, 迭代优化算法

Abstract:

Traditional multidimensional scaling method achieves low-dimensional embedding， which maintains the topological structure of data points but ignores the discriminability of the low-dimensional embedding itself. Based on this， an unsupervised discriminative feature learning method based on multidimensional scaling method named Discriminative MultiDimensional Scaling model （DMDS） was proposed to discover the cluster structure while learning the low-dimensional data representation. DMDS can make the low-dimensional embeddings of the same cluster closer to make the learned data representation be more discriminative. Firstly， a new objective function corresponding to DMDS was designed， reflecting that the learned data representation could maintain the topology and enhance discriminability simultaneously. Secondly， the objective function was reasoned and solved， and a corresponding iterative optimization algorithm was designed according to the reasoning process. Finally， comparison experiments were carried out on twelve public datasets in terms of average accuracy and average purity of clustering. Experimental results show that DMDS outperforms the original data representation and the traditional multidimensional scaling model based on the comprehensive evaluation of Friedman statistics， the low-dimensional embeddings learned by DMDS are more discriminative.

Key words: discriminative feature learning, multidimensional scaling, dimensionality reduction, fuzzy clustering, iterative optimization algorithm

中图分类号:

TP391.4

唐海涛, 王红军, 李天瑞. 判别多维标度特征学习[J]. 计算机应用, 2023, 43(5): 1323-1329.

Haitao TANG, Hongjun WANG, Tianrui LI. Discriminative multidimensional scaling for feature learning[J]. Journal of Computer Applications, 2023, 43(5): 1323-1329.

图/表 6

表1 符号说明

Tab. 1 Symbol notations

符号	含义	符号	含义
$N$	数据点个数	$X = [x 1, x 2, …, x N] ∈ R n × N$	原始数据矩阵
$n$	原始数据表示的维数	$Y = [y 1, y 2, …, y N] ∈ R l × N$	投影后的数据矩阵
$l$	学习到的低维数据表示维数	$W ∈ R n × l$	投影矩阵
$C$	簇个数	$S = [s i j] ∈ R N × N$	非负对称的权重矩阵
$m$	模糊指数权重	$U = [u i k] ∈ R N × C$	隶属度矩阵
$α$	E₁项损失的权重	$V = [v 1, v 2, …, v C] ∈ R l × C$	簇中心矩阵
$β$	E₂项损失的权重	D =［ $d i j$ ］ $∈ R N × N$	原始数据的距离矩阵
		$D ̂ = [d ̂ i j] ∈ R N × N$	低维数据表示的距离矩阵

表1 符号说明

Tab. 1 Symbol notations

符号	含义	符号	含义
$N$	数据点个数	$X = [x 1, x 2, …, x N] ∈ R n × N$	原始数据矩阵
$n$	原始数据表示的维数	$Y = [y 1, y 2, …, y N] ∈ R l × N$	投影后的数据矩阵
$l$	学习到的低维数据表示维数	$W ∈ R n × l$	投影矩阵
$C$	簇个数	$S = [s i j] ∈ R N × N$	非负对称的权重矩阵
$m$	模糊指数权重	$U = [u i k] ∈ R N × C$	隶属度矩阵
$α$	E₁项损失的权重	$V = [v 1, v 2, …, v C] ∈ R l × C$	簇中心矩阵
$β$	E₂项损失的权重	D =［ $d i j$ ］ $∈ R N × N$	原始数据的距离矩阵
		$D ̂ = [d ̂ i j] ∈ R N × N$	低维数据表示的距离矩阵

表2 实验数据集

Tab. 2 Experimental datasets

数据集	索引	样本数	特征数	类簇数	数据集	索引	样本数	特征数	类簇数
voituretuning	01	879	899	3	bubble	07	879	892	3
border	02	840	892	3	banana	08	840	892	3
bicycle	03	844	892	3	bus	09	910	892	3
building	04	911	892	3	vistawallpaper	10	799	899	3
banner	05	860	892	3	CNAE-9	11	1 080	856	9
wallpaper2	06	919	899	3	QSAR_AR	12	1 687	1 024	2

表3 不同数据表示下的平均聚类准确率

Tab. 3 Average clustering accuracy under different data representations

索引	KM	AP	DP	PMDS-KM	PMDS-AP	PMDS-DP	DMDS-KM	DMDS-AP	DMDS-DP	Avg	PMDS-Avg	DMDS-Avg
01	0.450 5	0.538 1	0.466 4	0.442 3	0.526 8	0.453 0	0.484 6	0.568 1	0.564 9	0.485 0	0.474 0	0.539 2
02	0.504 7	0.444 0	0.442 8	0.509 2	0.437 5	0.413 4	0.542 1	0.559 6	0.560 7	0.463 8	0.453 4	0.554 1
03	0.432 4	0.542 6	0.409 9	0.472 6	0.538 8	0.412 7	0.520 8	0.514 9	0.522 9	0.461 6	0.474 7	0.519 5
04	0.517 0	0.619 1	0.462 1	0.407 7	0.478 7	0.446 8	0.565 3	0.632 6	0.534 1	0.532 7	0.444 4	0.577 3
05	0.466 2	0.460 4	0.818 6	0.452 5	0.571 1	0.778 4	0.565 0	0.776 7	0.795 3	0.581 7	0.600 7	0.712 3
06	0.420 0	0.463 5	0.457 0	0.417 9	0.478 2	0.458 9	0.442 8	0.492 9	0.509 9	0.446 8	0.451 7	0.481 9
07	0.420 9	0.456 2	0.464 1	0.426 3	0.480 3	0.464 9	0.432 3	0.490 3	0.439 1	0.447 0	0.457 2	0.453 9
08	0.476 1	0.403 5	0.421 4	0.474 7	0.427 2	0.413 0	0.484 5	0.438 0	0.434 5	0.433 7	0.438 3	0.452 3
09	0.452 7	0.654 9	0.445 0	0.447 6	0.459 8	0.444 3	0.437 3	0.671 4	0.600 0	0.517 5	0.450 6	0.569 5
10	0.470 5	0.390 4	0.488 1	0.475 8	0.464 2	0.461 8	0.490 6	0.438 2	0.534 4	0.449 7	0.467 2	0.487 7
11	0.463 9	0.118 5	0.337 0	0.450 9	0.119 4	0.300 0	0.529 6	0.188 0	0.335 2	0.306 5	0.290 1	0.350 9
12	0.665 7	0.572 6	0.725 0	0.660 3	0.619 4	0.718 4	0.684 6	0.823 4	0.637 2	0.654 4	0.666 0	0.715 1

表4 不同数据表示下的平均聚类纯度

Tab. 4 Average clustering purity under different data representations

索引	KM	AP	DP	PMDS-KM	PMDS-AP	PMDS-DP	DMDS-KM	DMDS-AP	DMDS-DP	Avg	PMDS-Avg	DMDS-Avg
01	0.639 3	0.639 3	0.639 3	0.639 3	0.639 3	0.639 3	0.639 3	0.639 3	0.639 3	0.639 3	0.639 3	0.639 3
02	0.564 2	0.445 2	0.447 6	0.564 8	0.445 1	0.446 0	0.560 9	0.565 9	0.561 9	0.485 7	0.485 3	0.562 9
03	0.545 0	0.547 3	0.545 0	0.545 1	0.548 4	0.545 0	0.560 0	0.545 0	0.546 2	0.545 8	0.546 2	0.550 4
04	0.714 5	0.715 6	0.714 5	0.714 5	0.714 7	0.714 5	0.714 5	0.714 5	0.714 5	0.714 9	0.714 6	0.714 5
05	0.937 2	0.937 2	0.937 2	0.937 2	0.937 2	0.937 2	0.937 2	0.937 2	0.937 2	0.937 2	0.937 2	0.937 2
06	0.570 1	0.577 8	0.562 5	0.562 5	0.563 0	0.565 0	0.575 6	0.573 4	0.562 5	0.570 1	0.563 5	0.570 5
07	0.500 5	0.497 1	0.496 0	0.509 7	0.514 2	0.496 0	0.558 5	0.500 1	0.496 0	0.497 9	0.506 6	0.518 2
08	0.484 5	0.432 1	0.427 3	0.483 8	0.439 5	0.428 9	0.492 8	0.440 4	0.470 2	0.448 0	0.450 7	0.467 8
09	0.625 2	0.654 9	0.624 1	0.624 8	0.624 1	0.624 3	0.652 7	0.674 7	0.624 1	0.634 7	0.624 4	0.650 5
10	0.644 5	0.632 0	0.632 0	0.649 1	0.632 5	0.633 1	0.664 5	0.632 0	0.634 5	0.636 2	0.638 2	0.643 7
11	0.490 7	0.119 4	0.344 4	0.489 8	0.119 4	0.310 2	0.555 6	0.191 7	0.344 4	0.318 2	0.306 5	0.363 9
12	0.882 0	0.882 0	0.882 0	0.882 0	0.882 0	0.882 0	0.882 0	0.882 0	0.882 0	0.882 0	0.882 0	0.882 0

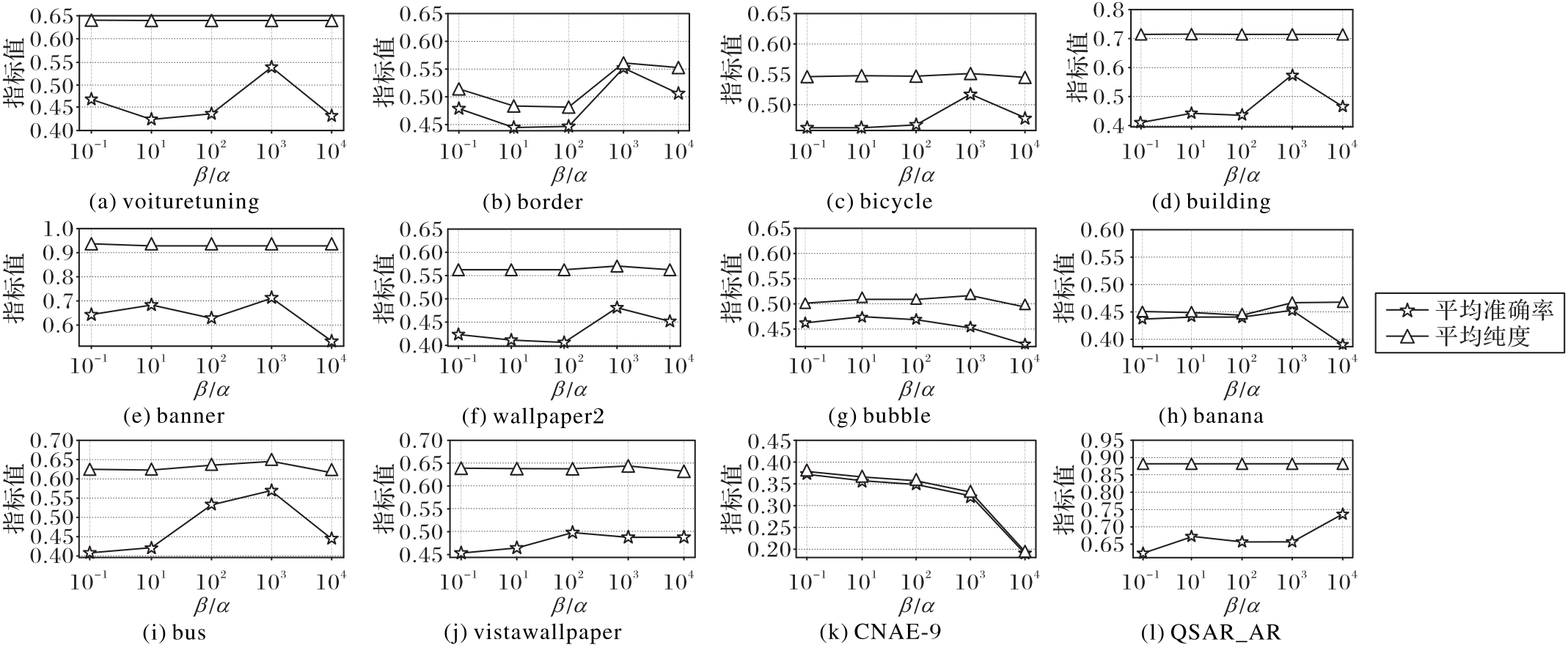
图1 DMDS在12个数据集上在不同β与α的比值下的平均准确率和平均纯度对比

Fig. 1 Average clustering accuracy and purity comparison of DMDS on 12 datasets with different ratios between β and α

图2 DMDS与PMDS运行时间的对比

Fig. 2 Running time comparison of DMDS and PMDS

参考文献 30

1	ZHANG Z， LI F Z， ZHAO M B， et al. Joint low-rank and sparse principal feature coding for enhanced robust representation and visual classification［J］. IEEE Transactions on Image Processing， 2016， 25（6）： 2429-2443. 10.1109/tip.2016.2547180
2	陈宏宇，邓德祥，颜佳，等. 基于显著性语义区域加权的图像检索算法［J］. 计算机应用， 2019， 39（1）：136-142. 10.11772/j.issn.1001-9081.2018051150
	CHEN H Y， DENG D X， YAN J， et al. Image retrieval algorithm based on saliency semantic region weighting［J］. Journal of Computer Applications， 2019， 39（1）： 136-142. 10.11772/j.issn.1001-9081.2018051150
3	范莉莉，卢桂馥，唐肝翌，等. 基于Hessian正则化和非负约束的低秩表示子空间聚类算法［J］. 计算机应用， 2022， 42（1）：115-122. 10.11772/j.issn.1001-9081.2021071181
	FAN L L， LU G F， TANG G Y， et al. Low-rank representation subspace clustering method based on Hessian regularization and non-negative constraint［J］. Journal of Computer Applications， 2022， 42（1）： 115-122. 10.11772/j.issn.1001-9081.2021071181
4	WOLD S， ESBENSEN K， GELADI P. Principal component analysis［J］. Chemometrics and Intelligent Laboratory Systems， 1987， 2（1/2/3）： 37-52. 10.1016/0169-7439(87)80084-9
5	ZHANG D Q， ZHOU Z H， CHEN S C. Semi-supervised dimensionality reduction［C］// Proceedings of the 2007 SIAM International Conference on Data Mining. Philadelphia， PA： SIAM， 2007： 629-634. 10.1137/1.9781611972771.73
6	MARTINEZ A M， KAK A C. PCA versus LDA［J］. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2001， 23（2）： 228-233. 10.1109/34.908974
7	ROWEIS S T， SAUL L K. Nonlinear dimensionality reduction by locally linear embedding［J］. Science， 2000， 290（5500）： 2323-2326. 10.1126/science.290.5500.2323
8	BORG I， GROENEN P J F. Modern Multidimensional Scaling： Theory and Applications［M］. 2nd ed. New York： Springer， 2005： 37-50.
9	BELKIN M， NIYOGI P. Laplacian Eigenmaps for dimensionality reduction and data representation［J］. Neural Computation， 2003， 15（6）： 1373-1396. 10.1162/089976603321780317
10	BENGIO Y， PAIEMENT J F， VINCENT P， et al . Out-of-sample extensions for LLE， ISOMAP， MDS， Eigenmaps， and spectral clustering［C］// Proceedings of the 16th International Conference on Neural Information Processing Systems. Cambridge： MIT Press， 2003： 177-184.
11	HE X F， NIYOGI P. Locality preserving projections［C］// Proceedings of the 16th International Conference on Neural Information Processing Systems. Cambridge： MIT Press， 2003： 153-160.
12	HE X F， CAI D， YAN S C， et al. Neighborhood preserving embedding［C］// Proceedings of the 10th IEEE International Conference on Computer Vision — Volume Ⅱ. Piscataway： IEEE， 2005： 1208-1213. 10.1109/iccv.2005.167
13	WEBB A R. Multidimensional scaling by iterative majorization using radial basis functions［J］. Pattern Recognition， 1995， 28（5）： 753-759. 10.1016/0031-3203(94)00135-9
14	DE LEEUW J. Convergence of the majorization method for multidimensional scaling［J］. Journal of Classification， 1988， 5（2）： 163-180. 10.1007/bf01897162
15	BISWAS S， BOWYER K W， FLYNN P J. Multidimensional scaling for matching low-resolution face images［J］. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2012， 34（10）： 2019-2030. 10.1109/tpami.2011.278
16	BISWAS S， AGGARWAL G， FLYNN P J， et al. Pose-robust recognition of low-resolution face images［J］. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2013， 35（12）： 3037-3049. 10.1109/tpami.2013.68
17	YANG F W， YANG W M， GAO R Q， et al. Discriminative multidimensional scaling for low-resolution face recognition［J］. IEEE Signal Processing Letters， 2018， 25（3）： 388-392. 10.1109/lsp.2017.2746658
18	LIKAS A， VLASSIS N， VERBEEK J J. The global k-means clustering algorithm［J］. Pattern Recognition， 2003， 36（2）： 451-461. 10.1016/s0031-3203(02)00060-2
19	FREY B J， DUECK D. Clustering by passing messages between data points［J］. Science， 2007， 315（5814）： 972-976. 10.1126/science.1136800
20	RODRIGUEZ A， LAIO A. Clustering by fast search and find of density peaks［J］. Science， 2014， 344（6191）： 1492-1496. 10.1126/science.1242072
21	BEZDEK J C， EHRLICH R， FULL W. FCM： the fuzzy c-means clustering algorithm［J］. Computers and Geosciences， 1984， 10（2/3）： 191-203. 10.1016/0098-3004(84)90020-7
22	WU K L， YANG M S. Alternative c-means clustering algorithms［J］. Pattern Recognition， 2002， 35（10）： 2267-2278. 10.1016/s0031-3203(01)00197-2
23	HOU C P， NIE F P， YI D Y， et al. Discriminative embedded clustering： a framework for grouping high-dimensional data［J］. IEEE Transactions on Neural Networks and Learning Systems， 2015， 26（6）： 1287-1299. 10.1109/tnnls.2014.2337335
24	LI R Y， ZHANG L F， DU B. A robust dimensionality reduction and matrix factorization framework for data clustering［J］. Pattern Recognition Letters， 2019， 128： 440-446. 10.1016/j.patrec.2019.10.006
25	NIE F P， ZHAO X W， WANG R， et al. Fuzzy K-Means clustering with discriminative embedding［J］. IEEE Transactions on Knowledge and Data Engineering， 2022， 34（3）： 1221-1230. 10.1109/tkde.2020.2995748
26	HUANG H C， CHUANG Y Y， CHEN C S. Multiple kernel fuzzy clustering［J］. IEEE Transactions on Fuzzy Systems， 2012， 20（1）： 120-134. 10.1109/tfuzz.2011.2170175
27	GOLUB G H， VAN LOAN C F. Matrix Computations［M］. 4th ed. Baltimore， MD： Johns Hopkins University Press， 2013： 488-493.
28	LI H， WANG M， HUA X S. MSRA-MM 2.0： a large-scale web multimedia dataset［C］// Proceedings of the 2009 IEEE International Conference on Data Mining Workshops. Piscataway： IEEE， 2009： 164-169. 10.1109/icdmw.2009.46
29	YANG Z R， OJA E. Linear and nonlinear projective nonnegative matrix factorization［J］. IEEE Transactions on Neural Networks， 2010， 21（5）： 734-749. 10.1109/tnn.2010.2041361
30	GARCÍA S， FERNÁNDEZ A， LUENGO J， et al. Advanced nonparametric tests for multiple comparisons in the design of experiments in computational intelligence and data mining： experimental analysis of power［J］. Information Sciences， 2010， 180（10）： 2044-2064. 10.1016/j.ins.2009.12.010

[1]	孟圣洁, 于万钧, 陈颖. 最大相关和最大差异的高维数据特征选择算法[J]. 《计算机应用》唯一官方网站, 2024, 44(3): 767-771.
[2]	赖星锦, 郑致远, 杜晓颜, 徐莎, 杨晓君. 基于超像素锚图二重降维的高光谱聚类算法[J]. 《计算机应用》唯一官方网站, 2022, 42(7): 2088-2093.
[3]	王基厚, 林培光, 周佳倩, 李庆涛, 张燕, 蹇木伟. 结合公司财务报表数据的股票指数预测方法[J]. 《计算机应用》唯一官方网站, 2021, 41(12): 3632-3636.
[4]	张阳, 王小宁. 基于Word2Vec词嵌入和高维生物基因选择遗传算法的文本特征选择方法[J]. 《计算机应用》唯一官方网站, 2021, 41(11): 3151-3155.
[5]	郭曙杰, 李志华, 蔺凯青. 云环境下基于模糊隶属度的虚拟机放置算法[J]. 计算机应用, 2020, 40(5): 1374-1381.
[6]	王锦凯, 贾旭. 基于加权正交约束非负矩阵分解的车脸识别算法[J]. 计算机应用, 2020, 40(4): 1050-1055.
[7]	李东博, 黄铝文. 重加权稀疏主成分分析算法及其在人脸识别中的应用[J]. 计算机应用, 2020, 40(3): 717-722.
[8]	来杰, 王晓丹, 李睿, 赵振冲. 基于去噪自编码器的极限学习机[J]. 计算机应用, 2019, 39(6): 1619-1625.
[9]	郭旭东, 李小敏, 敬如雪, 高玉琢. 基于改进的稀疏去噪自编码器的入侵检测[J]. 计算机应用, 2019, 39(3): 769-773.
[10]	韩忠华, 毕开元, 司雯, 吕哲. 基于谱分析的密度峰值快速聚类算法[J]. 计算机应用, 2019, 39(2): 409-413.
[11]	王鑫, 张鑫, 宁晨. 基于多特征降维和迁移学习的红外人体目标识别方法[J]. 计算机应用, 2019, 39(12): 3490-3495.
[12]	杨东海, 林敏敏, 张文杰, 杨敬民. 无监督混阶栈式稀疏自编码器的图像分类学习[J]. 计算机应用, 2019, 39(12): 3420-3425.
[13]	胡星辰, 申映华, 吴克宇, 程光权, 刘忠. 模糊规则模型的粒度性能指标评估方法[J]. 计算机应用, 2019, 39(11): 3114-3119.
[14]	杨国锋, 戴家才, 刘向君, 吴晓龙, 田延妮. 基于核模糊聚类的动态多子群协作骨干粒子群优化[J]. 计算机应用, 2018, 38(9): 2568-2574.
[15]	李昆仑, 关立伟, 郭昌隆. 基于聚类和改进共生演算法的云任务调度策略[J]. 计算机应用, 2018, 38(3): 707-714.

判别多维标度特征学习

Discriminative multidimensional scaling for feature learning

RichHTML

PDF

可视化

摘要/Abstract

引用本文

使用本文

图/表 6

参考文献 30

相关文章 15

编辑推荐

Metrics