《计算机应用》唯一官方网站 ›› 2023, Vol. 43 ›› Issue (5): 1355-1364.DOI: 10.11772/j.issn.1001-9081.2022030420
所属专题: 第九届中国数据挖掘会议(CCDM 2022)
收稿日期:2022-04-01
修回日期:2022-05-20
接受日期:2022-05-30
发布日期:2023-05-08
出版日期:2023-05-10
通讯作者:
张庆科
作者简介:高昊(1996—),男,山东淄博人,硕士研究生,CCF会员,主要研究方向:进化计算、群体智能基金资助:
Hao GAO, Qingke ZHANG( ), Xianglong BU, Junqing LI, Huaxiang ZHANG
), Xianglong BU, Junqing LI, Huaxiang ZHANG
Received:2022-04-01
Revised:2022-05-20
Accepted:2022-05-30
Online:2023-05-08
Published:2023-05-10
Contact:
Qingke ZHANG
About author:GAO Hao, born in 1996, M. S. candidate. His research interests include evolutionary computing, swarm intelligence.Supported by:摘要:
针对教与学优化(TLBO)算法在处理优化问题时存在搜索不均衡、易陷入局部最优、综合求解性能弱等缺陷,提出一种基于均衡优化与莱维飞行策略的改进教与学优化算法ELMTLBO。首先设计精英均衡引导策略,通过种群中多个精英个体的均衡引导提高算法的全局寻优能力;其次在TLBO算法的学习者阶段后,利用自适应权重策略对莱维飞行产生的步长进行自适应缩量,以提高种群局部寻优能力,增强个体对复杂环境的自适应性;最后设计了变异算子池逃逸策略,通过多个变异算子的协同引导,提升算法的种群多样性。为验证算法改进的有效性,将EMLTLBO算法与侏儒猫鼬优化算法(DMOA)等先进的智能优化算法以及平衡教与学优化(BTLBO)算法、标准TLBO等同类型算法在15个国际测试函数上进行综合收敛性能比较。统计实验结果表明,与先进的智能优化算法和TLBO算法变体相比,ELMTLBO算法能够有效平衡其搜索能力,不但有效求解单峰和多峰问题,而且在复杂多峰问题上仍有显著的寻优能力。在不同策略的共同作用下,ELMTLBO算法的综合优化性能突出,全局收敛性能较为稳定。此外,ELMTLBO算法成功应用于基于隐马尔可夫模型(HMM)的多序列比对(MSA)问题中,优化后得到的高质量对齐序列可用于疾病诊断、基因溯源等,可为生物信息学提供算法支撑。
中图分类号:
高昊, 张庆科, 卜降龙, 李俊青, 张化祥. 基于协同变异与莱维飞行策略的教与学优化算法及其应用[J]. 计算机应用, 2023, 43(5): 1355-1364.
Hao GAO, Qingke ZHANG, Xianglong BU, Junqing LI, Huaxiang ZHANG. Teaching-learning-based optimization algorithm based on cooperative mutation and Lévy flight strategy and its application[J]. Journal of Computer Applications, 2023, 43(5): 1355-1364.
| 函数 | 函数名 | 搜索范围 | 适应度值 | |
|---|---|---|---|---|
单峰 函数 | F1 | Sphere Function | [-100,100] | 0 |
| F2 | Schwefel's Problem 1.2 | [-100,100] | 0 | |
| F3 | Schwefel's Problem 1.2 With Noise | [-32,32] | 0 | |
| F4 | Schwefel's Problem 2.21 | [-5,5] | 0 | |
| F5 | Schwefel's Problem 2.22 | [-10,10] | 0 | |
| F6 | High Conditioned Elliptic Function | [-3,1] | 0 | |
| F7 | Step Function | [-10,10] | 0 | |
多峰 函数 | F8 | Schwefel Function | [-500,500] | 0 |
| F9 | Rosenbrock's Function | [-10,10] | 0 | |
| F10 | Quartic Function | [ | 0 | |
| F11 | Griewank's Function | [-600,600] | 0 | |
| F12 | Ackley's Function | [-32,32] | 0 | |
| F13 | Rastrign's Function | [-5.12,5.12] | 0 | |
| F14 | Rastrign's Noncontinue Function | [-5.12,5.12] | 0 | |
| F15 | Weierstrass Function | [-100,100] | 0 | |
表1 测试函数
Tab. 1 Test functions
| 函数 | 函数名 | 搜索范围 | 适应度值 | |
|---|---|---|---|---|
单峰 函数 | F1 | Sphere Function | [-100,100] | 0 |
| F2 | Schwefel's Problem 1.2 | [-100,100] | 0 | |
| F3 | Schwefel's Problem 1.2 With Noise | [-32,32] | 0 | |
| F4 | Schwefel's Problem 2.21 | [-5,5] | 0 | |
| F5 | Schwefel's Problem 2.22 | [-10,10] | 0 | |
| F6 | High Conditioned Elliptic Function | [-3,1] | 0 | |
| F7 | Step Function | [-10,10] | 0 | |
多峰 函数 | F8 | Schwefel Function | [-500,500] | 0 |
| F9 | Rosenbrock's Function | [-10,10] | 0 | |
| F10 | Quartic Function | [ | 0 | |
| F11 | Griewank's Function | [-600,600] | 0 | |
| F12 | Ackley's Function | [-32,32] | 0 | |
| F13 | Rastrign's Function | [-5.12,5.12] | 0 | |
| F14 | Rastrign's Noncontinue Function | [-5.12,5.12] | 0 | |
| F15 | Weierstrass Function | [-100,100] | 0 | |
| 函数 | 指标 | DMOA | WSO | INFO | CHIO | EO | SSA | Jaya | ELMTLBO |
|---|---|---|---|---|---|---|---|---|---|
| F1 | Mean | 1.05E-010 | 1.55E-021 | 2.99E-057 | 4.98E+000 | 0.00E+000 | 1.16E-008 | 2.58E-049 | 0.00E+000 |
| Std | 5.47E-011 | 1.66E-021 | 1.28E-057 | 3.10E+000 | 0.00E+000 | 1.89E-009 | 6.77E-049 | 0.00E+000 | |
| F2 | Mean | 1.77E+005 | 7.45E-001 | 4.73E-054 | 1.39E+004 | 2.34E-210 | 1.17E-006 | 6.62E+004 | 0.00E+000 |
| Std | 2.89E+004 | 8.27E-001 | 4.93E-054 | 2.01E+003 | 0.00E+000 | 3.01E-007 | 1.38E+004 | 0.00E+000 | |
| F3 | Mean | 2.22E+004 | 1.05E+002 | 6.73E-054 | 4.91E+003 | 1.76E-169 | 6.09E+002 | 8.88E+003 | 0.00E+000 |
| Std | 3.53E+003 | 3.34E+001 | 6.05E-054 | 5.64E+002 | 0.00E+000 | 2.35E+002 | 1.04E+003 | 0.00E+000 | |
| F4 | Mean | 3.56E+000 | 5.49E-003 | 2.18E-029 | 4.37E-001 | 9.67E-219 | 3.50E-001 | 1.21E-001 | 0.00E+000 |
| Std | 3.12E-001 | 2.48E-003 | 1.25E-029 | 1.04E-001 | 0.00E+000 | 1.22E-001 | 4.91E-002 | 0.00E+000 | |
| F5 | Mean | 3.14E-008 | 2.55E-015 | 2.92E-028 | 1.19E+000 | 0.00E+000 | 1.14E+000 | 2.05E-028 | 0.00E+000 |
| Std | 7.22E-008 | 1.75E-015 | 6.14E-029 | 5.47E-001 | 0.00E+000 | 1.05E+000 | 3.05E-028 | 0.00E+000 | |
| F6 | Mean | 6.73E-010 | 1.51E-019 | 2.35E-052 | 1.40E+001 | 0.00E+000 | 1.16E+003 | 1.31E-045 | 0.00E+000 |
| Std | 3.35E-010 | 3.69E-019 | 1.67E-052 | 8.93E+000 | 0.00E+000 | 4.20E+002 | 3.75E-045 | 0.00E+000 | |
| F7 | Mean | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 1.83E+001 | 3.15E+000 | 0.00E+000 |
| Std | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 8.47E+000 | 2.32E+000 | 0.00E+000 | |
| F8 | Mean | 7.39E+003 | 6.42E+003 | 6.52E+003 | 8.42E+002 | 6.31E+003 | 8.36E+003 | 5.00E+003 | 5.06E-011 |
| Std | 1.57E+003 | 1.05E+003 | 6.58E+002 | 5.23E+002 | 9.19E+002 | 1.05E+003 | 5.98E+003 | 3.58E-011 | |
| F9 | Mean | 1.10E+002 | 6.98E+001 | 2.00E+000 | 1.42E+002 | 3.87E+001 | 4.54E+001 | 1.10E-004 | 4.08E-008 |
| Std | 7.68E+001 | 2.74E+001 | 1.30E+000 | 2.43E+001 | 1.31E+000 | 2.31E+000 | 3.18E-004 | 5.09E-008 | |
| F10 | Mean | 2.53E+000 | 7.08E-030 | 2.44E-113 | 8.38E+001 | 0.00E+000 | 2.89E-016 | 5.30E-060 | 0.00E+000 |
| Std | 1.61E+000 | 1.12E-029 | 3.17E-113 | 8.9EE+001 | 0.00E+000 | 1.15E-016 | 1.45E-059 | 0.00E+000 | |
| F11 | Mean | 3.80E-010 | 2.42E-002 | 0.00E+000 | 6.01E-001 | 0.00E+000 | 5.67E-003 | 6.16E-003 | 0.00E+000 |
| Std | 2.96E-010 | 4.09E-002 | 0.00E+000 | 4.68E-001 | 0.00E+000 | 5.45E-003 | 7.27E-003 | 0.00E+000 | |
| F12 | Mean | 6.27E-006 | 1.77E-011 | 0.00E+000 | 5.66E-002 | 3.55E-015 | 2.23E+000 | 2.87E+000 | 0.00E+000 |
| Std | 3.34E-006 | 1.15E-011 | 0.00E+000 | 7.43E-002 | 0.00E+000 | 5.65E-001 | 6.05E+000 | 0.00E+000 | |
| F13 | Mean | 2.58E+002 | 2.08E-014 | 0.00E+000 | 3.32E+000 | 0.00E+000 | 9.55E+001 | 2.09E+002 | 0.00E+000 |
| Std | 8.30E+001 | 5.79E-014 | 0.00E+000 | 2.75E+000 | 0.00E+000 | 2.70E+001 | 1.17E+002 | 0.00E+000 | |
| F14 | Mean | 3.06E+002 | 1.49E-013 | 0.00E+000 | 3.66E+000 | 0.00E+000 | 1.41E+002 | 3.59E+002 | 0.00E+000 |
| Std | 6.43E+001 | 3.09E-013 | 0.00E+000 | 3.61E+000 | 0.00E+000 | 3.64E+001 | 3.80E+001 | 0.00E+000 | |
| F15 | Mean | 5.18E+001 | 4.97E-014 | 0.00E+000 | 9.84E-001 | 0.00E+000 | 2.50E+001 | 4.15E+000 | 0.00E+000 |
| Std | 5.57E+000 | 1.80E-014 | 0.00E+000 | 8.60E-001 | 0.00E+000 | 4.52E+000 | 2.03E+000 | 0.00E+000 |
表2 ELMTLBO与不同类型算法针对50维问题在基准函数上的性能比较
Tab. 2 Performance comparison of ELMTLBO and different types of algorithms on benchmark functions for 50-dimensional problems
| 函数 | 指标 | DMOA | WSO | INFO | CHIO | EO | SSA | Jaya | ELMTLBO |
|---|---|---|---|---|---|---|---|---|---|
| F1 | Mean | 1.05E-010 | 1.55E-021 | 2.99E-057 | 4.98E+000 | 0.00E+000 | 1.16E-008 | 2.58E-049 | 0.00E+000 |
| Std | 5.47E-011 | 1.66E-021 | 1.28E-057 | 3.10E+000 | 0.00E+000 | 1.89E-009 | 6.77E-049 | 0.00E+000 | |
| F2 | Mean | 1.77E+005 | 7.45E-001 | 4.73E-054 | 1.39E+004 | 2.34E-210 | 1.17E-006 | 6.62E+004 | 0.00E+000 |
| Std | 2.89E+004 | 8.27E-001 | 4.93E-054 | 2.01E+003 | 0.00E+000 | 3.01E-007 | 1.38E+004 | 0.00E+000 | |
| F3 | Mean | 2.22E+004 | 1.05E+002 | 6.73E-054 | 4.91E+003 | 1.76E-169 | 6.09E+002 | 8.88E+003 | 0.00E+000 |
| Std | 3.53E+003 | 3.34E+001 | 6.05E-054 | 5.64E+002 | 0.00E+000 | 2.35E+002 | 1.04E+003 | 0.00E+000 | |
| F4 | Mean | 3.56E+000 | 5.49E-003 | 2.18E-029 | 4.37E-001 | 9.67E-219 | 3.50E-001 | 1.21E-001 | 0.00E+000 |
| Std | 3.12E-001 | 2.48E-003 | 1.25E-029 | 1.04E-001 | 0.00E+000 | 1.22E-001 | 4.91E-002 | 0.00E+000 | |
| F5 | Mean | 3.14E-008 | 2.55E-015 | 2.92E-028 | 1.19E+000 | 0.00E+000 | 1.14E+000 | 2.05E-028 | 0.00E+000 |
| Std | 7.22E-008 | 1.75E-015 | 6.14E-029 | 5.47E-001 | 0.00E+000 | 1.05E+000 | 3.05E-028 | 0.00E+000 | |
| F6 | Mean | 6.73E-010 | 1.51E-019 | 2.35E-052 | 1.40E+001 | 0.00E+000 | 1.16E+003 | 1.31E-045 | 0.00E+000 |
| Std | 3.35E-010 | 3.69E-019 | 1.67E-052 | 8.93E+000 | 0.00E+000 | 4.20E+002 | 3.75E-045 | 0.00E+000 | |
| F7 | Mean | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 1.83E+001 | 3.15E+000 | 0.00E+000 |
| Std | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 8.47E+000 | 2.32E+000 | 0.00E+000 | |
| F8 | Mean | 7.39E+003 | 6.42E+003 | 6.52E+003 | 8.42E+002 | 6.31E+003 | 8.36E+003 | 5.00E+003 | 5.06E-011 |
| Std | 1.57E+003 | 1.05E+003 | 6.58E+002 | 5.23E+002 | 9.19E+002 | 1.05E+003 | 5.98E+003 | 3.58E-011 | |
| F9 | Mean | 1.10E+002 | 6.98E+001 | 2.00E+000 | 1.42E+002 | 3.87E+001 | 4.54E+001 | 1.10E-004 | 4.08E-008 |
| Std | 7.68E+001 | 2.74E+001 | 1.30E+000 | 2.43E+001 | 1.31E+000 | 2.31E+000 | 3.18E-004 | 5.09E-008 | |
| F10 | Mean | 2.53E+000 | 7.08E-030 | 2.44E-113 | 8.38E+001 | 0.00E+000 | 2.89E-016 | 5.30E-060 | 0.00E+000 |
| Std | 1.61E+000 | 1.12E-029 | 3.17E-113 | 8.9EE+001 | 0.00E+000 | 1.15E-016 | 1.45E-059 | 0.00E+000 | |
| F11 | Mean | 3.80E-010 | 2.42E-002 | 0.00E+000 | 6.01E-001 | 0.00E+000 | 5.67E-003 | 6.16E-003 | 0.00E+000 |
| Std | 2.96E-010 | 4.09E-002 | 0.00E+000 | 4.68E-001 | 0.00E+000 | 5.45E-003 | 7.27E-003 | 0.00E+000 | |
| F12 | Mean | 6.27E-006 | 1.77E-011 | 0.00E+000 | 5.66E-002 | 3.55E-015 | 2.23E+000 | 2.87E+000 | 0.00E+000 |
| Std | 3.34E-006 | 1.15E-011 | 0.00E+000 | 7.43E-002 | 0.00E+000 | 5.65E-001 | 6.05E+000 | 0.00E+000 | |
| F13 | Mean | 2.58E+002 | 2.08E-014 | 0.00E+000 | 3.32E+000 | 0.00E+000 | 9.55E+001 | 2.09E+002 | 0.00E+000 |
| Std | 8.30E+001 | 5.79E-014 | 0.00E+000 | 2.75E+000 | 0.00E+000 | 2.70E+001 | 1.17E+002 | 0.00E+000 | |
| F14 | Mean | 3.06E+002 | 1.49E-013 | 0.00E+000 | 3.66E+000 | 0.00E+000 | 1.41E+002 | 3.59E+002 | 0.00E+000 |
| Std | 6.43E+001 | 3.09E-013 | 0.00E+000 | 3.61E+000 | 0.00E+000 | 3.64E+001 | 3.80E+001 | 0.00E+000 | |
| F15 | Mean | 5.18E+001 | 4.97E-014 | 0.00E+000 | 9.84E-001 | 0.00E+000 | 2.50E+001 | 4.15E+000 | 0.00E+000 |
| Std | 5.57E+000 | 1.80E-014 | 0.00E+000 | 8.60E-001 | 0.00E+000 | 4.52E+000 | 2.03E+000 | 0.00E+000 |
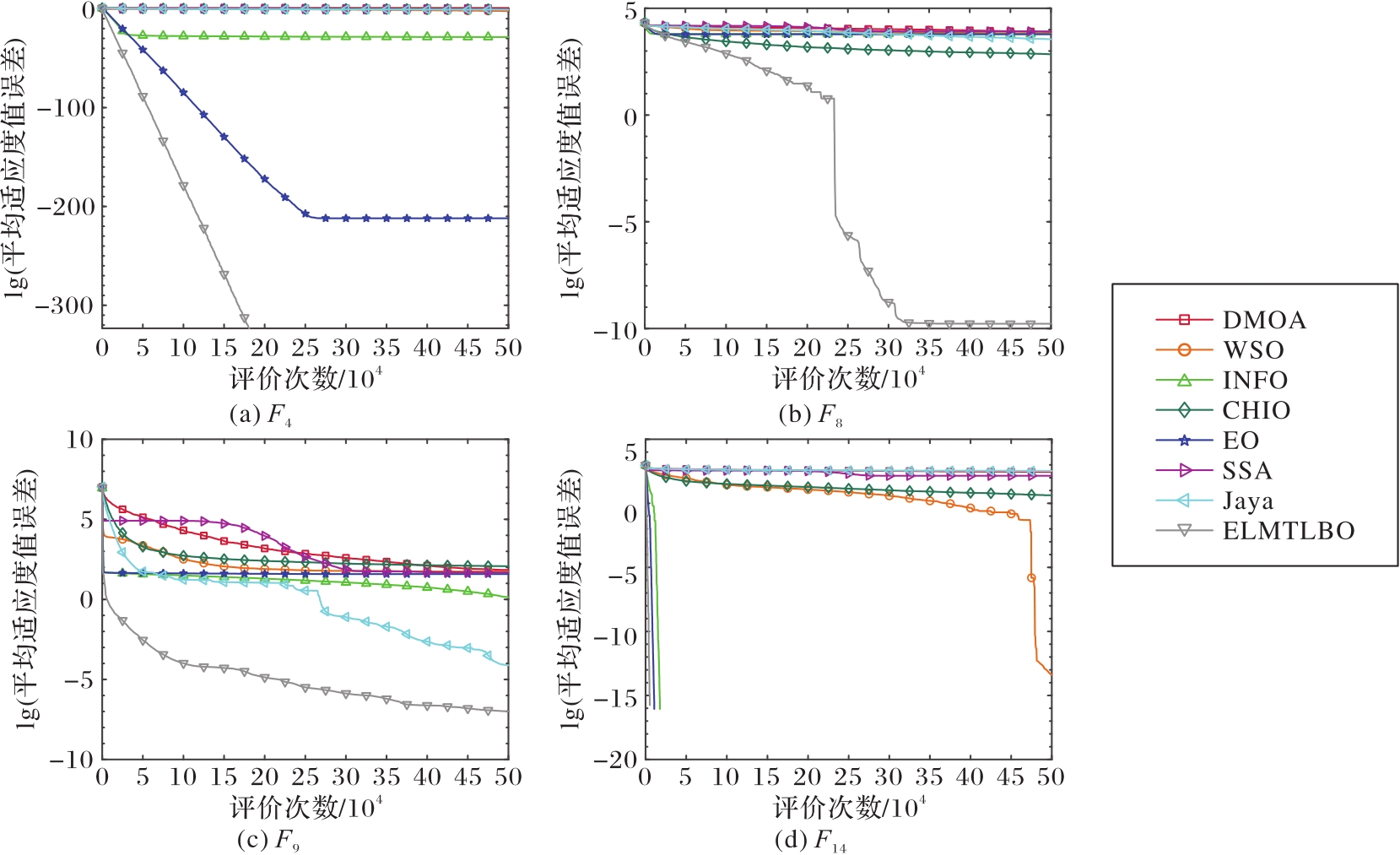
图2 不同类型算法针对50维问题在基准函数上的平均适应度值误差收敛曲线比较
Fig. 2 Comparison of fitness convergence curves of different types of algorithms on benchmark functions for 50-dimensional problems
| 函数 | 指标 | BTLBO | CTLBO | ETLBO | EFTLBO | OTLBO | TLBOCIW | TLBO | ELMTLBO |
|---|---|---|---|---|---|---|---|---|---|
| F1 | Mean | 6.33E-006 | 0.00E+000 | 1.47E-001 | 1.75E-001 | 0.00E+000 | 2.92E-197 | 0.00E+000 | 0.00E+000 |
| Std | 1.97E-006 | 0.00E+000 | 1.97E-001 | 2.30E-001 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 | |
| F2 | Mean | 2.07E+002 | 0.00E+000 | 7.09E+000 | 5.60E+000 | 1.83E-260 | 7.23E-041 | 1.98E-277 | 0.00E+000 |
| Std | 3.17E+001 | 0.00E+000 | 8.83E+000 | 9.14E+000 | 0.00E+000 | 3.23E-040 | 0.00E+000 | 0.00E+000 | |
| F3 | Mean | 8.41E+003 | 0.00E+000 | 1.87E+000 | 9.83E-001 | 2.06E-163 | 1.57E-166 | 6.10E-199 | 0.00E+000 |
| Std | 2.45E+003 | 0.00E+000 | 1.68E+000 | 1.46E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 | |
| F4 | Mean | 1.69E-002 | 9.88E-324 | 1.39E-002 | 1.89E-002 | 9.88E-324 | 4.94E-324 | 9.88E-324 | 0.00E+000 |
| Std | 4.03E-003 | 0.00E+000 | 1.59E-002 | 1.19E-002 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 | |
| F5 | Mean | 1.04E-002 | 0.00E+000 | 7.91E-002 | 1.04E-001 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 |
| Std | 2.81E-003 | 0.00E+000 | 1.22E-001 | 1.52E-001 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 | |
| F6 | Mean | 2.83E-002 | 0.00E+000 | 2.02E-001 | 9.39E-002 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 |
| Std | 1.29E-002 | 0.00E+000 | 3.68E-001 | 2.26E-001 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 | |
| F7 | Mean | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 |
| Std | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 | |
| F8 | Mean | 5.80E+003 | 1.19E-005 | 6.10E+002 | 3.33E+002 | 1.87E+004 | 1.64E+004 | 1.98E+004 | 2.11E-009 |
| Std | 8.37E+002 | 1.68E-005 | 1.27E+002 | 8.08E+002 | 6.05E+004 | 3.60E+002 | 1.10E+002 | 1.33E-009 | |
| F9 | Mean | 2.25E+002 | 4.60E-005 | 9.71E+001 | 9.78E+001 | 8.21E+001 | 9.14E+001 | 8.30E+001 | 1.87E-006 |
| Std | 7.54E+001 | 5.29E-005 | 1.97E+000 | 1.59E+000 | 1.61E+000 | 8.41E-001 | 1.56E+000 | 1.61E-006 | |
| F10 | Mean | 6.18E-010 | 0.00E+000 | 1.78E+000 | 2.65E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 |
| Std | 3.51E-010 | 0.00E+000 | 3.07E+000 | 4.19E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 | |
| F11 | Mean | 2.64E-002 | 0.00E+000 | 6.30E-002 | 6.29E-002 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 |
| Std | 2.54E-002 | 0.00E+000 | 1.10E-001 | 1.03E-001 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 | |
| F12 | Mean | 6.07E+000 | 0.00E+000 | 6.91E-002 | 7.15E-002 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 |
| Std | 2.48E+000 | 0.00E+000 | 1.15E-001 | 1.42E-001 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 | |
| F13 | Mean | 6.07E+000 | 0.00E+000 | 6.92E-002 | 7.15E-002 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 |
| Std | 2.48E+000 | 0.00E+000 | 1.15E-001 | 1.42E-001 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 | |
| F14 | Mean | 8.45E+000 | 0.00E+000 | 8.97E-002 | 5.13E-002 | 4.33E+001 | 0.00E+000 | 3.64E+001 | 0.00E+000 |
| Std | 2.54E+000 | 0.00E+000 | 1.39E-001 | 1.04E-001 | 2.90E+001 | 0.00E+000 | 2.58E+001 | 0.00E+000 | |
| F15 | Mean | 6.75E-001 | 0.00E+000 | 5.99E-001 | 6.15E-001 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 |
| Std | 8.79E-002 | 0.00E+000 | 6.10E-001 | 5.35E-001 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 |
表3 ELMTLBO与同类型改进算法针对100维问题在基准函数上的性能比较
Tab. 3 Performance comparison of ELMTLBO and improved algorithms of the same type on benchmark functions for 100-dimensional problems
| 函数 | 指标 | BTLBO | CTLBO | ETLBO | EFTLBO | OTLBO | TLBOCIW | TLBO | ELMTLBO |
|---|---|---|---|---|---|---|---|---|---|
| F1 | Mean | 6.33E-006 | 0.00E+000 | 1.47E-001 | 1.75E-001 | 0.00E+000 | 2.92E-197 | 0.00E+000 | 0.00E+000 |
| Std | 1.97E-006 | 0.00E+000 | 1.97E-001 | 2.30E-001 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 | |
| F2 | Mean | 2.07E+002 | 0.00E+000 | 7.09E+000 | 5.60E+000 | 1.83E-260 | 7.23E-041 | 1.98E-277 | 0.00E+000 |
| Std | 3.17E+001 | 0.00E+000 | 8.83E+000 | 9.14E+000 | 0.00E+000 | 3.23E-040 | 0.00E+000 | 0.00E+000 | |
| F3 | Mean | 8.41E+003 | 0.00E+000 | 1.87E+000 | 9.83E-001 | 2.06E-163 | 1.57E-166 | 6.10E-199 | 0.00E+000 |
| Std | 2.45E+003 | 0.00E+000 | 1.68E+000 | 1.46E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 | |
| F4 | Mean | 1.69E-002 | 9.88E-324 | 1.39E-002 | 1.89E-002 | 9.88E-324 | 4.94E-324 | 9.88E-324 | 0.00E+000 |
| Std | 4.03E-003 | 0.00E+000 | 1.59E-002 | 1.19E-002 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 | |
| F5 | Mean | 1.04E-002 | 0.00E+000 | 7.91E-002 | 1.04E-001 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 |
| Std | 2.81E-003 | 0.00E+000 | 1.22E-001 | 1.52E-001 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 | |
| F6 | Mean | 2.83E-002 | 0.00E+000 | 2.02E-001 | 9.39E-002 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 |
| Std | 1.29E-002 | 0.00E+000 | 3.68E-001 | 2.26E-001 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 | |
| F7 | Mean | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 |
| Std | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 | |
| F8 | Mean | 5.80E+003 | 1.19E-005 | 6.10E+002 | 3.33E+002 | 1.87E+004 | 1.64E+004 | 1.98E+004 | 2.11E-009 |
| Std | 8.37E+002 | 1.68E-005 | 1.27E+002 | 8.08E+002 | 6.05E+004 | 3.60E+002 | 1.10E+002 | 1.33E-009 | |
| F9 | Mean | 2.25E+002 | 4.60E-005 | 9.71E+001 | 9.78E+001 | 8.21E+001 | 9.14E+001 | 8.30E+001 | 1.87E-006 |
| Std | 7.54E+001 | 5.29E-005 | 1.97E+000 | 1.59E+000 | 1.61E+000 | 8.41E-001 | 1.56E+000 | 1.61E-006 | |
| F10 | Mean | 6.18E-010 | 0.00E+000 | 1.78E+000 | 2.65E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 |
| Std | 3.51E-010 | 0.00E+000 | 3.07E+000 | 4.19E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 | |
| F11 | Mean | 2.64E-002 | 0.00E+000 | 6.30E-002 | 6.29E-002 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 |
| Std | 2.54E-002 | 0.00E+000 | 1.10E-001 | 1.03E-001 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 | |
| F12 | Mean | 6.07E+000 | 0.00E+000 | 6.91E-002 | 7.15E-002 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 |
| Std | 2.48E+000 | 0.00E+000 | 1.15E-001 | 1.42E-001 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 | |
| F13 | Mean | 6.07E+000 | 0.00E+000 | 6.92E-002 | 7.15E-002 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 |
| Std | 2.48E+000 | 0.00E+000 | 1.15E-001 | 1.42E-001 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 | |
| F14 | Mean | 8.45E+000 | 0.00E+000 | 8.97E-002 | 5.13E-002 | 4.33E+001 | 0.00E+000 | 3.64E+001 | 0.00E+000 |
| Std | 2.54E+000 | 0.00E+000 | 1.39E-001 | 1.04E-001 | 2.90E+001 | 0.00E+000 | 2.58E+001 | 0.00E+000 | |
| F15 | Mean | 6.75E-001 | 0.00E+000 | 5.99E-001 | 6.15E-001 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 |
| Std | 8.79E-002 | 0.00E+000 | 6.10E-001 | 5.35E-001 | 0.00E+000 | 0.00E+000 | 0.00E+000 | 0.00E+000 |
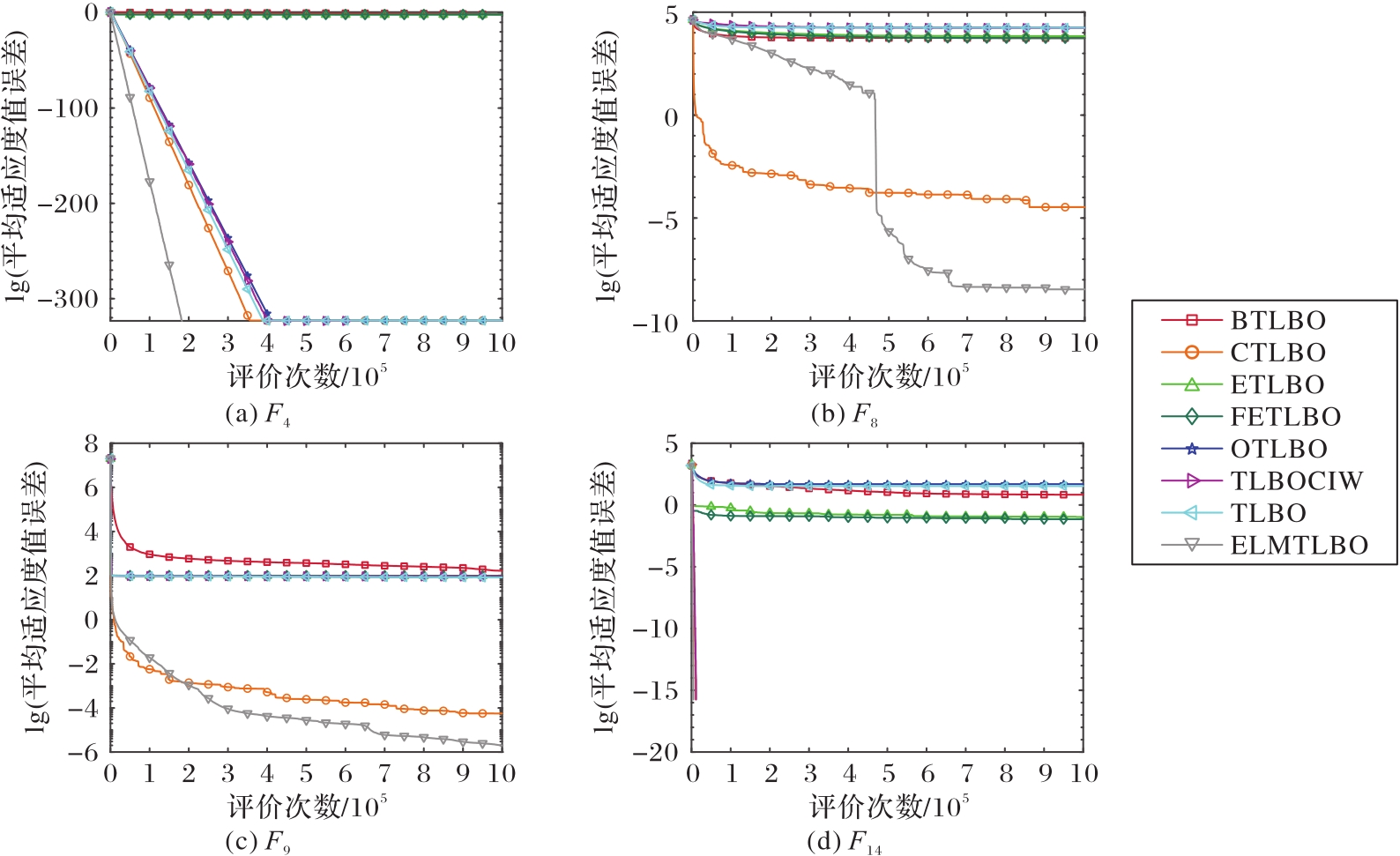
图3 ELMTLBO与TLBO算法变体针对100维问题在基准函数上的平均适应度值误差收敛曲线比较
Fig. 3 Comparison of fitness error convergence curves of ELMTLBO and TLBO algorithm variants on benchmark functions for 100-dimensional problems
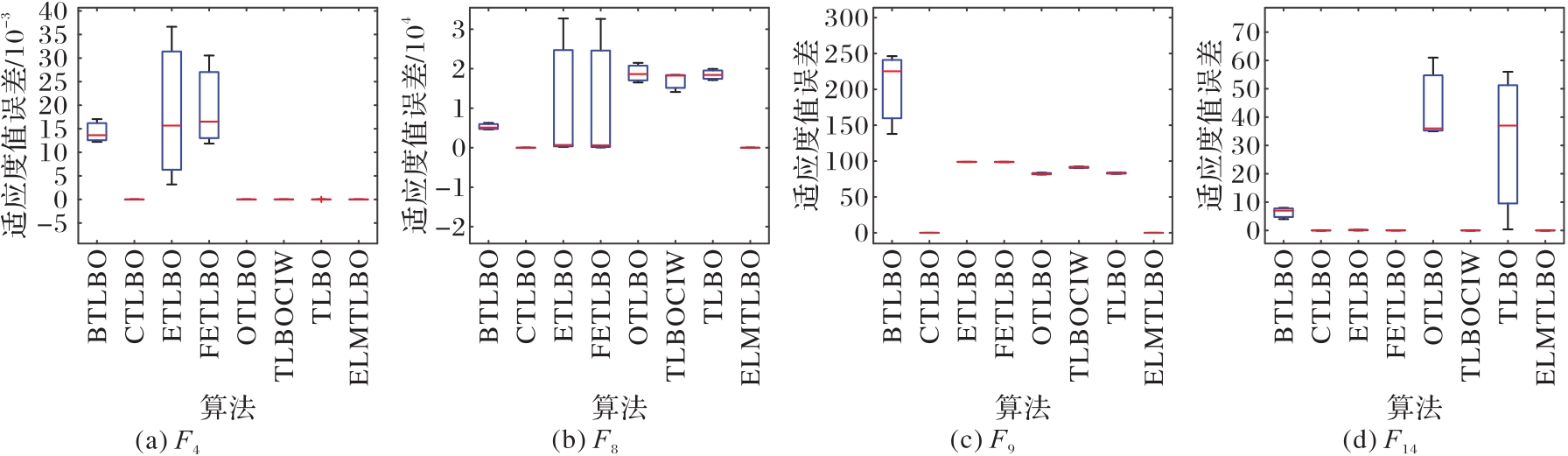
图4 ELMTLBO与经典TLBO改进算法针对100维问题在基准函数上的箱图比较
Fig. 4 Comparison of box plots of ELMTLBO and classic improved algorithms of TLBO on benchmark functions for 100-dimensional problems
| 数据集 | 函数 | TLBOE | TLBOL | TLBOM | TLBO | ELMTLBO |
|---|---|---|---|---|---|---|
| CEC2017 | 2.71E+003 | 5.74E+002 | 1.06E+003 | 3.61E+003 | 1.46E+002 | |
| CEC2005 | 3.19E+003 | 3.32E+003 | 5.48E+002 | 3.37E+003 | 2.85E+002 | |
| CEC2005 | 1.49E+002 | 8.17E+001 | 1.09E+002 | 1.09E+002 | 6.90E+001 | |
| CEC2005 | 3.34E+001 | 3.26E+001 | 2.89E+001 | 3.10E+001 | 2.34E+001 | |
| CEC2017 | 1.72E+004 | 1.03E+004 | 1.16E+004 | 1.20E+004 | 2.56E+003 |
表4 不同改进策略的结果对比
Tab. 4 Comparison of results of different improvement strategies
| 数据集 | 函数 | TLBOE | TLBOL | TLBOM | TLBO | ELMTLBO |
|---|---|---|---|---|---|---|
| CEC2017 | 2.71E+003 | 5.74E+002 | 1.06E+003 | 3.61E+003 | 1.46E+002 | |
| CEC2005 | 3.19E+003 | 3.32E+003 | 5.48E+002 | 3.37E+003 | 2.85E+002 | |
| CEC2005 | 1.49E+002 | 8.17E+001 | 1.09E+002 | 1.09E+002 | 6.90E+001 | |
| CEC2005 | 3.34E+001 | 3.26E+001 | 2.89E+001 | 3.10E+001 | 2.34E+001 | |
| CEC2017 | 1.72E+004 | 1.03E+004 | 1.16E+004 | 1.20E+004 | 2.56E+003 |
| 算法 | 参数设置 |
|---|---|
| wPSO | |
| GA | |
| EO | |
| TLBO | |
| ELMTLBO |
表5 算法参数设置
Tab. 5 Algorithm parameter setting
| 算法 | 参数设置 |
|---|---|
| wPSO | |
| GA | |
| EO | |
| TLBO | |
| ELMTLBO |
| Name | lengthdata | LSEQ(m,n) | Dim | wPSO | GA | EO | TLBO | ELMTLBO | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Score | T/s | Score | T/s | Score | T/s | Score | T/s | Score | T/s | ||||
| 451c | 5 | (210,261) | 5 345 | 7.65E+002 | 846 | 7.76E+002 | 608 | 3.56E+002 | 785 | 1.51E+002 | 1 469 | 8.60E+002 | 1 823 |
| 1ad2 | 4 | (609,639) | 13 046 | 9.53E+002 | 949 | 1.05E+003 | 1 041 | 1.11E+003 | 1 430 | 9.39E+000 | 2 307 | 1.24E+003 | 3 572 |
| kinase1 | 5 | (74,86) | 1 775 | 2.70E+002 | 499 | 3.01E+002 | 464 | 3.62E+002 | 339 | 2.67E+002 | 837 | 3.20E+002 | 1 146 |
| kinase2 | 5 | (789,828) | 16 905 | 2.20E+003 | 1 229 | 2.34E+003 | 1 262 | 2.48E+003 | 1 238 | 2.57E+002 | 2 542 | 2.70E+003 | 5 411 |
表6 不同算法的多序列比对结果
Tab. 6 Results of multiple sequence alignment of different algorithms
| Name | lengthdata | LSEQ(m,n) | Dim | wPSO | GA | EO | TLBO | ELMTLBO | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Score | T/s | Score | T/s | Score | T/s | Score | T/s | Score | T/s | ||||
| 451c | 5 | (210,261) | 5 345 | 7.65E+002 | 846 | 7.76E+002 | 608 | 3.56E+002 | 785 | 1.51E+002 | 1 469 | 8.60E+002 | 1 823 |
| 1ad2 | 4 | (609,639) | 13 046 | 9.53E+002 | 949 | 1.05E+003 | 1 041 | 1.11E+003 | 1 430 | 9.39E+000 | 2 307 | 1.24E+003 | 3 572 |
| kinase1 | 5 | (74,86) | 1 775 | 2.70E+002 | 499 | 3.01E+002 | 464 | 3.62E+002 | 339 | 2.67E+002 | 837 | 3.20E+002 | 1 146 |
| kinase2 | 5 | (789,828) | 16 905 | 2.20E+003 | 1 229 | 2.34E+003 | 1 262 | 2.48E+003 | 1 238 | 2.57E+002 | 2 542 | 2.70E+003 | 5 411 |
| 1 | RAO R V, SAVSANI V J, VAKHARIA D P. Teaching-learning-based optimization: an optimization method for continuous non-linear large scale problems[J]. Information Sciences, 2012, 183(1): 1-15. 10.1016/j.ins.2011.08.006 |
| 2 | BHOOKYA J, JATOTH R K. Fractional order PID controller design for multivariable systems using TLBO[J]. Chemical Product and Process Modeling, 2020, 15(2): No.20190061. |
| 3 | ALIZADEH M, RODRIGUEZ R, BAUMAN J, et al. Optimal design of integrated heat pipe air-cooled system using TLBO algorithm for SiC MOSFET converters[J]. IEEE Open Journal of Power Electronics, 2020, 1: 103-112. 10.1109/ojpel.2020.2985700 |
| 4 | NOSRATIAN S, MORADKHANI M, TAVAKOLI M B. Fuzzy-based reliability prediction model for secure routing protocol using GA and TLBO for implementation of black hole attacks in WSN[J]. Journal of Circuits, Systems and Computers, 2021, 30(6): No.2150098. 10.1142/s0218126621500985 |
| 5 | KASHYAP A K, PANDEY A, PARHI D R, et al. Path optimization for multiple humanoid robot using TLBO based ANFIS controller in obscure environment[J]. Materials Today: Proceedings, 2021, 47(Pt 11): 2677-2684. 10.1016/j.matpr.2021.02.756 |
| 6 | GAVARRAJU L N J, PAVAN K K. Sequence alignment by Modified Teaching Learning Based Optimization algorithm (M-TLBO)[M]// KUMAR A, MOZAR S. ICCCE 2020: Proceedings of the 3rd International Conference on Communications and Cyber Physical Engineering, LNEE 698. Singapore: Springer, 2021: 1441-1454. 10.1007/978-981-15-7961-5_131 |
| 7 | THAHER T, MAFARJA M, TURABIEH H, et al. Teaching learning-based optimization with evolutionary binarization schemes for tackling feature selection problems[J]. IEEE Access, 2021, 9: 41082-41103. 10.1109/access.2021.3064799 |
| 8 | DEB S, HOUSSEIN E H, SAID M, et al. Performance of turbulent flow of water optimization on economic load dispatch problem[J]. IEEE Access, 2021, 9: 77882-77893. 10.1109/access.2021.3083531 |
| 9 | PRASAD C D, BISWAL M, RAY P. Enhancing fault detection function in wind farm-integrated power network using teaching learning-based optimization technique[J]. International Transactions on Electrical Energy Systems, 2021, 31(10): No.e12735. 10.1002/2050-7038.12735 |
| 10 | CHIRANJEEVI K, JENA U, RAO M V N. Image compression based on adaptive image thresholding by maximising Shannon or fuzzy entropy using teaching learning based optimisation[J]. International Journal of Advanced Intelligence Paradigms, 2021, 18(2): 193-231. 10.1504/ijaip.2021.10035158 |
| 11 | WANG X Y, LI Y P. Chaotic image encryption algorithm based on hybrid multi-objective particle swarm optimization and DNA sequence[J]. Optics and Lasers in Engineering, 2021, 137: No.106393. 10.1016/j.optlaseng.2020.106393 |
| 12 | ROY P K, PAUL C, SULTANA S. Oppositional teaching learning based optimization approach for combined heat and power dispatch[J]. International Journal of Electrical Power and Energy Systems, 2014, 57: 392-403. 10.1016/j.ijepes.2013.12.006 |
| 13 | CHEN D B, LU R Q, ZOU F, et al. Teaching-learning-based optimization with variable-population scheme and its application for ANN and global optimization[J]. Neurocomputing, 2016, 173(Pt 3): 1096-1111. 10.1016/j.neucom.2015.08.068 |
| 14 | YU K J, WANG X, WANG Z L. Constrained optimization based on improved teaching-learning-based optimization algorithm[J]. Information Sciences, 2016, 352/353: 61-78. 10.1016/j.ins.2016.02.054 |
| 15 | WANG Z, LU R Q, CHEN D B, et al. An experience information teaching-learning-based optimization for global optimization[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2016, 46(9): 1202-1214. 10.1109/tsmc.2015.2503406 |
| 16 | TAHERI A, RahimiZADEH K, RAO R V. An efficient balanced teaching-learning-based optimization algorithm with individual restarting strategy for solving global optimization problems[J]. Information Sciences, 2021, 576: 68-104. 10.1016/j.ins.2021.06.064 |
| 17 | HE X Z, RAO Y Q, HUANG J D. A novel algorithm for economic load dispatch of power systems[J]. Neurocomputing, 2016, 171: 1454-1461. 10.1016/j.neucom.2015.07.107 |
| 18 | RAO R V, PATEL V. An elitist teaching-learning-based optimization algorithm for solving complex constrained optimization problems[J]. International Journal of Industrial Engineering Computations, 2012, 3(4): 535-560. 10.5267/j.ijiec.2012.03.007 |
| 19 | 于坤杰,王昕,王振雷. 基于反馈的精英教与学优化算法[J]. 自动化学报, 2014, 40(9):1976-1983. |
| YU K J, WANG X, WANG Z L. Elitist teaching-learning-based optimization algorithm based on feedback[J]. Acta Automatica Sinica, 2014, 40(9): 1976-1983. | |
| 20 | NIU P F, MA Y P, YAN S S. A modified teaching-learning-based optimization algorithm for numerical function optimization[J]. International Journal of Machine Learning and Cybernetics, 2019, 10(6): 1357-1371. 10.1007/s13042-018-0815-8 |
| 21 | WU Z S, FU W P, XUE R. Nonlinear inertia weighted teaching-learning-based optimization for solving global optimization problem[J]. Computational Intelligence and Neuroscience, 2015, 2015: No.292576. 10.1155/2015/292576 |
| 22 | CAO J X, LUO J X. A study on SVM based on the weighted elitist teaching-learning-based optimization and application in the fault diagnosis of chemical process[J]. MATEC Web of Conferences, 2015, 22: No.05016. 10.1051/matecconf/20152205016 |
| 23 | COELHO D B P, RODRIGUES L R. A chaotic inertia weight TLBO applied to troubleshooting optimization problems[C]// Proceedings of the 2020 IEEE Congress on Evolutionary Computation. Piscataway: IEEE, 2020: 1-8. 10.1109/cec48606.2020.9185897 |
| 24 | ZOU F, CHEN D B, WANG J T. An improved teaching-learning-based optimization with the social character of PSO for global optimization[J]. Computational Intelligence and Neuroscience, 2016, 2016: No.4561507. 10.1155/2016/4561507 |
| 25 | OUYANG H B, MA G, LIU G Y, et al. Hybrid teaching-learning based optimization with harmony search for engineering optimization problems[C]// Proceedings of the 36th Chinese Control Conference. Piscataway: IEEE, 2017: 2714-2717. 10.23919/chicc.2017.8027774 |
| 26 | CHEN D B, ZOU F, WANG J T, et al. SAMCCTLBO: a multi-class cooperative teaching-learning-based optimization algorithm with simulated annealing[J]. Soft Computing, 2016, 20(5): 1921-1943. 10.1007/s00500-015-1613-9 |
| 27 | FARAMARZI A, HEIDARINEJAD M, STEPHENS B, et al. Equilibrium optimizer: a novel optimization algorithm[J]. Knowledge-Based Systems, 2020, 191: No.105190. 10.1016/j.knosys.2019.105190 |
| 28 | BROCKMANN D, HUFNAGEL L, GEISEL T. The scaling laws of human travel[J]. Nature, 2006, 439(7075): 462-465. 10.1038/nature04292 |
| 29 | RHEE I, SHIN M, HONG S, et al. On the Levy-walk nature of human mobility[J]. IEEE/ACM Transactions on Networking, 2011, 19(3): 630-643. 10.1109/tnet.2011.2120618 |
| 30 | YANG X S. Nature-Inspired Metaheuristic Algorithms[M]. 2nd ed. Frome: Luniver Press, 2010: 1-148. |
| 31 | YANG X S, DEB S. Cuckoo search via Lévy flights[C]// Proceedings of the 2009 World Congress on Nature and Biologically Inspired Computing. Piscataway: IEEE, 2009: 210-214. 10.1109/nabic15938.2009 |
| 32 | 郑洁锋,占红武,黄巍,等. Lévy Flight的发展和智能优化算法中的应用综述[J]. 计算机科学, 48(2): 190-206. 10.11896/jsjkx.200500142 |
| ZHENG J F, ZHAN H W, HUANG W, et al. Development of Lévy Flight and its application in intelligent optimization algorithm[J]. Computer Science, 2021, 48(2): 190-206. 10.11896/jsjkx.200500142 | |
| 33 | QIN A K, HUANG V L, SUGANTHAN P N. Differential evolution algorithm with strategy adaptation for global numerical optimization[J]. IEEE Transactions on Evolutionary Computation, 2009, 13(2): 398-417. 10.1109/tevc.2008.927706 |
| 34 | AGUSHAKA J O, EZUGWU A E, ABUALIGAH L. Dwarf mongoose optimization algorithm[J]. Computer Methods in Applied Mechanics and Engineering, 2022, 391: No.114570. 10.1016/j.cma.2022.114570 |
| 35 | BRAIK M, HAMMOURI A, ATWAN J, et al. White Shark Optimizer: a novel bio-inspired meta-heuristic algorithm for global optimization problems[J]. Knowledge-Based Systems, 2022, 243: No.108457. 10.1016/j.knosys.2022.108457 |
| 36 | AHMADIANFAR I, HEIDARI A A, NOSHADIAN S, et al. INFO: an efficient optimization algorithm based on weighted mean of vectors[J]. Expert Systems with Applications, 2022, 195: No.116516. 10.1016/j.eswa.2022.116516 |
| 37 | AL-BETAR M A, ALYASSERI Z A A, AWADALLAH M A, et al. Coronavirus herd immunity optimizer (CHIO)[J]. Neural Computing and Applications, 2021, 33(10): 5011-5042. 10.1007/s00521-020-05296-6 |
| 38 | MIRJALILI S, GANDOMI A H, MIRJALILI S Z, et al. Salp swarm algorithm: a bio-inspired optimizer for engineering design problems[J]. Advances in Engineering Software, 2017, 114: 163-191. 10.1016/j.advengsoft.2017.07.002 |
| 39 | RAO R V. Jaya: a simple and new optimization algorithm for solving constrained and unconstrained optimization problems[J]. International Journal of Industrial Engineering Computations, 2016, 7(1): 19-34. |
| 40 | 詹青. 基于隐马尔可夫模型的蛋白质多序列比对方法研究[D]. 哈尔滨:哈尔滨工业大学, 2019:1-4. |
| ZHAN Q. Research on protein multiple sequence alignment method based on hidden Markov model[D]. Harbin: Harbin Institute of Technology, 2019: 1-4. |
| [1] | 力尚龙, 刘建华, 贾鹤鸣. 融合多狩猎协调策略的爬行动物搜索算法[J]. 《计算机应用》唯一官方网站, 2024, 44(9): 2818-2828. |
| [2] | 李焱, 潘大志, 郑思情. 多车场带时间窗车辆路径问题的改良自适应大邻域搜索算法[J]. 《计算机应用》唯一官方网站, 2024, 44(6): 1897-1904. |
| [3] | 韦修喜, 彭茂松, 黄华娟. 基于多策略改进蝴蝶优化算法的无线传感网络节点覆盖优化[J]. 《计算机应用》唯一官方网站, 2024, 44(4): 1009-1017. |
| [4] | 欧云, 周恺卿, 尹鹏飞, 刘雪薇. 双收敛因子策略下的改进灰狼优化算法[J]. 《计算机应用》唯一官方网站, 2023, 43(9): 2679-2685. |
| [5] | 邱仲睿, 苗虹, 曾成碧. 多策略融合的改进黏菌算法[J]. 《计算机应用》唯一官方网站, 2023, 43(3): 812-819. |
| [6] | 马学森, 许雪梅, 蒋功辉, 乔焰, 周天保. 混合自适应粒子群工作流调度优化算法[J]. 《计算机应用》唯一官方网站, 2023, 43(2): 474-483. |
| [7] | 陈俊, 何庆, 李守玉. 基于黄金莱维引导机制的阿基米德优化算法[J]. 《计算机应用》唯一官方网站, 2022, 42(9): 2807-2815. |
| [8] | 张伟康, 刘升, 黄倩, 郭雨鑫. 考虑距离因素与精英进化策略的平衡优化器[J]. 《计算机应用》唯一官方网站, 2022, 42(6): 1844-1851. |
| [9] | 聂方鑫, 王宇嘉, 贾欣. 教与学信息交互粒子群优化算法[J]. 《计算机应用》唯一官方网站, 2022, 42(3): 874-882. |
| [10] | 雍欣, 高岳林, 赫亚华, 王惠敏. 多策略融合的改进萤火虫算法[J]. 《计算机应用》唯一官方网站, 2022, 42(12): 3847-3855. |
| [11] | 郭潇, 李春山, 张宇跃, 初佃辉. 基于自适应多目标强化学习的服务集成方法[J]. 《计算机应用》唯一官方网站, 2022, 42(11): 3500-3505. |
| [12] | 贾鹤鸣, 李瑶, 姜子超, 孙康健. 基于改进共生生物搜索算法的林火图像多阈值分割[J]. 计算机应用, 2021, 41(5): 1465-1470. |
| [13] | 王博, 刘连生, 韩绍程, 祝世兴. 基于多策略融合的混合多目标蝗虫优化算法[J]. 计算机应用, 2020, 40(9): 2670-2676. |
| [14] | 霍纬纲, 王慧芳. 基于自编码器和隐马尔可夫模型的时间序列异常检测方法[J]. 计算机应用, 2020, 40(5): 1329-1334. |
| [15] | 王金策, 邓越萍, 史明, 周云飞. 多时间尺度时间序列趋势预测[J]. 计算机应用, 2019, 39(4): 1046-1052. |
| 阅读次数 | ||||||
|
全文 |
|
|||||
|
摘要 |
|
|||||